The vibration behavior of axially moving material are involved in many engineering devices such as power transmission belt, magnetic tapes, paper tapes, thread lines, plastic web and aerial cable tramways. The dynamics of system can be differently modeled depending on the length, flexibility, and control objective of system considered. For instance, the dynamics of a moving cable of an elevator string equation, but that of a rubber belt in the traditional mill can be well represented by a belt equation. The difference between a string and a belt lies in whether the longitudinal elongation is considered or not.
In axially moving system, the transverse (lateral) vibration of the moving material often causes a serious problem in achieving good quality. It is also know that these vibrations are often caused by the eccentricity of a pulley, and/ or an irregular speed of the driving motor, and/ or a non-uniform material property, and/ or environmental disturbances. Since the quality requirement as well as the productivity in a production line is getting stricter, an active or a semi-active vibration control is nowadays seriously considered.
Boundary control of Axially Moving Steel Strip under a Spatiotemporally Varying Tension
The moving steel strip is modeled as a moving beam, in which the tension applied to the strip is a spatiotemporally varying function. The transverse vibration o the strip is controlled by a hydraulic touch roll actuator at the right boundary. The mathematical model of the system, which consists of hyperpolic partial differential equation describing the dynamics of the moving beam and an ordinary differential equation describing the actuator dynamics, is derived by using the Hamiltons principle for the systems of changing mass. The Lyapunov method is employed to design a boundary control law for ensuring the vibration reduction of the system in the presence of spatiotemporally varying tension. The exponential stability of the closed loop system of closed loop system under the boundary control is proved through the use of invariance principle and semigroup theory.
[Fig1. An axially moving strip in the zinc galvanizing line]
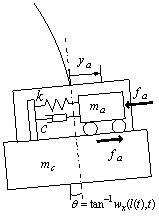
Adaptive Control of Axially Moving Systems
In this application, an adaptive control design for a 3-D crane is investigated. The control objectives in this paper are to move the gantry of a container crane to its target position and to suppress the transverse vibration of the payload. The crane system is modeled as an axially moving string equation, in which control inputs are applied at both ends, through the gantry and the payload. The dynamics of the moving string are derived using Hamiltons principle for systems with changing mass.
[Fig2. (a) An axially moving string with inputs at the gantry(b) The inclined payload and/ or payload positions.]
[(b) The inclined payload]